二個振ると偶数の方が多く出るサイコロはあるよという話
探偵ナイトスクープという番組で確率の話をしていたらしい.
nanigoto.hatenablog.jp
成田理論の説明はリンク先を見てもらうとして,番組の解説ではサイコロの例を出して理論を反駁していた.つまり,次の図のように(偶数)-(奇数)と(奇数)-(偶数)という出方があるから,和について偶数と奇数は同じ確率で出るという主張だ.
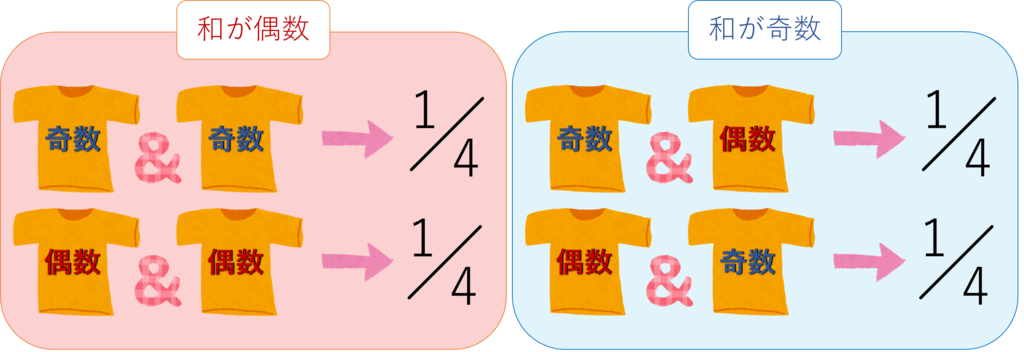
ところが,同じようなサイコロでも偶数の和が多く出るようなものが存在することが分かっている.それも目の出方が偏っているものではない,つまり公平なかつ偶数の和が多く出るサイコロだ.まずは次のような設定を考えよう.6つに区切られた箱に玉を入れてよく振ってあげる.すると玉は各仕切りに等しい確率で見つかるだろう.これを原始的なサイコロとして扱おう.もしくは,1から6番までの番号を振ったルーレットに玉を投入してよく回すと考えてもよい.
ここに図が入る***
同じ玉をもう一個この箱に加えて振れば,二つのサイコロを同時に振る状況が作れるだろう.果たしてこのときの結果はどうなるだろうか.
箱や玉が君の指でつまめるほどの大きさならば結果は君の予想通りだろう.しかし,玉として極めて小さい微粒子,それも光子や陽子といったボース粒子を使うと話は変わってくる.
ボース粒子を使ってこのサイコロの実験をした場合は,出目の組み合わせについて等確率でサイコロの値が決まる.つまり,(1)-(1)という目と(2)-(3)という目は等確率に出るのだ.このとき,下図に示すように各組み合わせを数えれば,和が偶数になるのは12通りで奇数になるのは9通りとなり,結局偶数の和が出る確率は4/7で奇数よりも大きい.

そんな微小な世界の話なんて我々には関係ないと思うかもしれない.しかし我々だって細かく見れば原子の集まりである.一体どうして微粒子が従う確率の法則*1と巨大なサイコロの従う確率法則が違うといえるだろうか?我々が素直に信じている確率の割り振り方*2は一体どこからやってくるのだろう?
結局,これらの確率の割り振りの確からしさは実験によって確かめるしかない.サイコロを何百回,何万回と振ったら我々のよく知る法則(古典的な法則)が出てくるが,対照的に微粒子を扱う実験では奇妙な組み合わせへの割り振りに現象が支配される(量子的な法則).もちろん,サッカー選手は十分大きい対象であるから従う確率法則はサイコロのものと同一だろう.でも,それは実験によって確かめられるものなのだ*3.この点では,実際に統計を見てみる姿勢は素晴らしいといえよう*4.
我々は微粒子に還元可能であるというのに,その微粒子の従う法則とは全く違う見た目の法則に支配されるという事実はいつ見ても興味深い.『小さくて単純なものがたくさん集まってびっくりするようなことをおこしてしまう!』ということなんだろうなあ.
http://www.gakushuin.ac.jp/~881791/d/1610.html#20
ご意見・ご感想・訂正などはコメント欄または@__pandaman64__までお願いします.
元ネタ:イアン・ハッキング『確率の出現』
確率という概念が現れる時代(1660年頃)についての科学史書.医術や錬金術などの「低級科学」とみなされてきた学問がいかに確率の形成に関わってきたかに詳しい.本編で出てきたボース粒子等の確率的性質が実験事実であることについては数行割かれているのみだが,自分にとっては本書の中でも一二を争うほど極めて響いた部分である.