#学門越え落ちたの私だ

ネタの鮮度落ちてない？

慶應大学理工学部には受験時に次の５つの学門を選んで入学します．

  1. 物理
  2. 数学
  3. 化学
  4. 機械
  5. 情報

１年生は進級時に学科を選ぶのですが，基本的には所属している学門の学科しか選択できません．異なる学門の学科へと進学するには，『学門越え』をする必要があります．

『学門越え』をする場合は，同じ学科へ『学門越え』する学生の内で成績が高い方から，特別な定員（通常の○％）分だけが進学することができます．

ぼくは学門５（情報系）から物理学科（学門１）に『学門越え』を申請し，今年の成績は以下の通りでした．

f:id:pandaman64:20160317022416p:plain

Aがたっぷりできれいだなあ（）物理学科の定員１名だけどいけるだろうなあ（）

結果は次の通り↓

f:id:pandaman64:20160317022422p:plain

(´･_･`)・・・

ぼくよりできる奴がいるのは知ってるけどよりにもよって物理学科に『学門越え』するような奴の中におりますかー

正直この成績で物理学科行けないの信じられないにゃあ　悲しいにゃあ

情報工学でやりたいこと見つかってません．「これやろうぜ！」みたいなの待ってます．Kinectで画像処理したり自作言語のコンパイラ作ったりしたことがあります．よろしくお願いします．

掛算の順序について（英語）

初等教育における掛算の順序固定教育について色々考えて文章の形にまとめたので置いておきます．
リンク：http://1drv.ms/1K6aQ1t
英語の講義の期末レポート用に書いたので英語です．日本語版は試験終了後気が向いたら書きます．

化学の勉強しなきゃ・・・

波動方程式の一般解

世間に出回っている波動方程式の解法は関数形を天下りに導入してなぜそれが一般解なのかを言わないものばかりだったので書いた．はてなブログは式番号が付いてないとレイアウトがおかしくなるので式に絵文字がついてますが無視してください．

波動方程式を解く

簡単のため，一次元波動方程式の一般解を求める．すなわち，C^2級関数\psi(x,t)について，偏微分方程式
\dfrac{\partial^2 \psi(x,t)}{{\partial t}^2} = c^2 \dfrac{\partial^2 \psi(x,t)}{{\partial x}^2}\tag{cは定数}
の一般解を求めたい．

まずは，次の変数変換を考える．
\begin{align} X = x + ct,&Y = x - ct \tag{☺} \end{align}
と置けば，
\begin{cases} \dfrac{\partial X}{\partial x} = 1 & \dfrac{\partial X}{\partial t} = c \\ \dfrac{\partial Y}{\partial x} = 1 & \dfrac{\partial Y}{\partial t} = -c \end{cases} \tag{☺}
を得る．(x,t)と(X,Y)は一対一対応するので，関数\psi(x,t)はX,Yを用いて\psi(X,Y)と表せる．

このとき，波動方程式の左辺は
\begin{align} \begin{aligned} \frac{\partial^2 \psi(X,Y)}{{\partial t}^2} &= \frac{\partial}{\partial t}\left(\frac{\partial X}{\partial t}\frac{\partial \psi}{\partial X}+\frac{\partial Y}{\partial t}\frac{\partial \psi}{\partial Y}\right) \\ &= c\frac{\partial}{\partial t}\left(\frac{\partial \psi}{\partial X}(X,Y)-\frac{\partial \psi}{\partial Y}(X,Y)\right) \\ &= c\left(\frac{\partial X}{\partial t}\frac{\partial^2 \psi}{{\partial X}^2}+\frac{\partial Y}{\partial t}\frac{\partial^2 \psi}{\partial Y\partial X}-\frac{\partial X}{\partial t}\frac{\partial^2 \psi}{\partial X\partial Y}-\frac{\partial Y}{\partial t}\frac{\partial^2 \psi}{{\partial Y}^2}\right) \\ &= c^2\left(\frac{\partial^2 \psi}{{\partial X}^2}-2\frac{\partial^2 \psi}{\partial X\partial Y}+\frac{\partial^2 \psi}{{\partial Y}^2}\right) \end{aligned} \tag{☺} \end{align}
となる．ただし，最後の式変形に\psiがC^2級であることを用いた．

右辺についても，
\begin{align} \begin{aligned} \frac{\partial^2 \psi(X,Y)}{{\partial x}^2} &= \frac{\partial}{\partial x}\left(\frac{\partial X}{\partial x}\frac{\partial \psi}{\partial X}+\frac{\partial Y}{\partial x}\frac{\partial \psi}{\partial Y}\right) \\ &= \frac{\partial}{\partial x}\left(\frac{\partial \psi}{\partial X}(X,Y)+\frac{\partial \psi}{\partial Y}(X,Y)\right) \\ &= \frac{\partial X}{\partial x}\frac{\partial^2 \psi}{{\partial X}^2}+\frac{\partial Y}{\partial x}\frac{\partial^2 \psi}{\partial Y\partial X}-\frac{\partial X}{\partial x}\frac{\partial^2 \psi}{\partial X\partial Y}-\frac{\partial Y}{\partial x}\frac{\partial^2 \psi}{{\partial Y}^2} \\ &= \frac{\partial^2 \psi}{{\partial X}^2}+2\frac{\partial^2 \psi}{\partial X\partial Y}+\frac{\partial^2 \psi}{{\partial Y}^2} \end{aligned} \tag{☺} \end{align}
となる．これらを両辺に代入すれば，
c^2\left(\dfrac{\partial^2 \psi}{{\partial X}^2}-2\dfrac{\partial^2 \psi}{\partial X\partial Y}+\dfrac{\partial^2 \psi}{{\partial Y}^2}\right) = c^2\left(\dfrac{\partial^2 \psi}{{\partial X}^2}+2\dfrac{\partial^2 \psi}{\partial X\partial Y}+\dfrac{\partial^2 \psi}{{\partial Y}^2}\right) \tag{☺}
であり，整理すれば
\dfrac{\partial^2 \psi}{\partial X\partial Y} = 0　\tag{☺}
を得る．高次元に拡張した際も，最終的にはこの式に到達する．この式は，\psiのC^2級性より，
\begin{cases} \dfrac{\partial}{\partial X}\dfrac{\partial \psi}{\partial Y} = 0\\ \dfrac{\partial}{\partial Y}\dfrac{\partial \psi}{\partial X} = 0 \end{cases} \tag{☺}
が共に成り立つことと同値．これを満たすような関数は，Xだけの関数f(X)とYだけの関数g(Y)で，
\begin{cases} \dfrac{\partial \psi}{\partial X} = f(X)\\ \dfrac{\partial \psi}{\partial Y} = g(Y) \end{cases} \tag{☺}
となる任意のf(X),g(Y)である．それぞれ積分すれば，f(X)とg(Y)の原始関数をそれぞれ
F(X)とG(Y)とおいて，
\begin{cases} \displaystyle\int\dfrac{\partial \psi}{\partial X}dX = F(X)\\ \displaystyle\int\dfrac{\partial \psi}{\partial Y}dY = G(Y) \end{cases} \tag{☺}
となるから，辺々足して，
\int\left(\dfrac{\partial \psi}{\partial X}dX+\dfrac{\partial \psi}{\partial Y}dY\right) = F(X) + G(Y) \tag{☺}
を得る．左辺はd\psiの全微分であるから*1，
\begin{aligned} \int d\psi &= F(X) + G(Y) \\ \psi &= F(X) + G(Y) \end{aligned} \tag{☺}
となり，変数変換を元に戻せば
\psi(x,t) = F(x + ct) + G(x - ct) \tag{☺}
を得る*2．定義より，F,GはC^2級の任意の関数．これが波動方程式の一般解である．

疑問

石を水面に投げ込んだ時の波って全然「平面」波に見えないんですけどどうなってるの？

*1:ここの議論適当

*2:積分定数は適当にF,Gに繰り込めばよい

定常電流の保存則が分かった

物理

この記事では定常電流の保存則が他の法則とどのような関係にあるのかを導出します．その後，導体の性質を用いてなぜ導体では定常電流の保存則が成立するかを説明します．

いくつか物理量を定義しておきましょう．

  • \rho : 電荷密度
  • \boldsymbol{E} : 電場
  • \boldsymbol{i} : 電流密度
  • \sigma : 電気伝導度

これらは各点で十分なめらかだと仮定します（偏微分の入れ替えのため）．

また，命題p,q,rに対して，
\begin{equation} p\overset{r}{\iff}q \tag{1} \end{equation}
と書いたときは，rが成立する条件においてpとqが同値，つまりp\land r\iff q\land rであることを指します．以下でバンバン使うので実例を見れば言いたいことが分かると思います．

定常電流の保存則

詳しい導出は前の記事を参照してください．pandaman64.hatenablog.jp

アンペール（・マクスウェル）の法則から
\begin{equation} \mathrm{div}\,\boldsymbol{i} = 0 \overset{アンペールの法則}{\iff} \dfrac{\partial \boldsymbol{E}}{\partial t} = 0. \tag{2} \end{equation}
電荷保存則から
\begin{equation} \mathrm{div}\,\boldsymbol{i} = 0 \overset{電荷保存則}{\iff} \dfrac{\partial \rho}{\partial t} = 0. \tag{3} \end{equation}
したがって，(2)(3)式から，
\mathrm{div}\,\boldsymbol{i} = 0 \overset{\substack{電荷保存則\\アンペールの法則}}{\iff} \dfrac{\partial \rho}{\partial t} = 0 \overset{\substack{電荷保存則\\アンペールの法則}}{\iff} \dfrac{\partial \boldsymbol{E}}{\partial t} = 0 \tag{4}
が言えます．言葉で言いかえれば，定常電流の保存則が成立することと電場が定常であることは同じ現象を指します．

導体を流れる定常電流

電場が定常であるという条件下において，導体内をミクロに考察することで，局所的なオームの法則が成立することが分かります．
\begin{equation} \text{「オームの法則」}\quad\quad\boldsymbol{i}\overset{電場が定常}{=}\sigma\boldsymbol{E} \tag{5} \end{equation}

(5)式を両辺を時間で偏微分しましょう．
\begin{equation} \text{「オームの法則」}\quad\quad\dfrac{\partial \boldsymbol{i}}{\partial t}\overset{電場が定常}{=}\sigma\dfrac{\partial\boldsymbol{E}}{\partial t} \tag{6} \end{equation}
ところが，オームの法則は電場が定常であるという条件下で導かれたのでした．つまり，(6)式は
\begin{equation} \dfrac{\partial \boldsymbol{i}}{\partial t}\overset{電場が定常}{=}0 \tag{7} \end{equation}
と書けます．したがって，定常電場内の導体には定常電流が流れるということが分かります．

最後に，(4)(7)式を用いれば，
\mathrm{div}\,\boldsymbol{i} = 0 \overset{\substack{電場が定常\\電荷保存則\\アンペールの法則}}{\iff} \dfrac{\partial \rho}{\partial t} = 0 \overset{\substack{電場が定常\\電荷保存則\\アンペールの法則}}{\iff} \dfrac{\partial \boldsymbol{i}}{\partial t} = 0 \tag{8}
となります．この同値関係が定常電流の保存則です．電場の定常性がこの法則に重要な役割を果たしていることが分かります．

課題

なんでふつうの回路が定常電場かどうか分かってないですね．定常電流分かってませんでした．でもここまでくれば後は電源を考慮に入れてのほんの一歩だと思いますし，説明の納得しやすさも大分良くなってきました（大学のテキストが言いたかったのもこういうことだと思う）．

オームの法則は導体の性質として前提に持ってきちゃいました．これはどの分野を学べば理解できるのでしょう．統計を使った物理学や量子力学になるのかなあ．

磁場についても色々言えると思いますが，磁場の性質はよく理解してないのでこれから解析したいですね．

定常電流の保存則：リアクション

夢にまで見た「全コメ返し」をやります．色々なご意見参考になりましたありがとうございます．他に思うことがあればなんでもぜひぜひお教えください．

電流はキルヒホッフの第一・第二法則を満たすように決まる


これはその通りで，電流一定の条件下で解いたからといって，必ず電流一定となるかは明らかではないです．

ただし，この場合はうまくいってくれます．電流の単位を持つ定数を適当にI_0と定めて，極板間距離x(t)=\varepsilon_0 SI_0 R/(Q_0 - It)となるように極板を動かすと，電流I=I_0が時間によらず成立することが示せます（計算は各自どうぞ）．

導線が電気的に中性な状態を保つはずだ

この言明こそが定常電流の保存則の帰結なんですが，たぶん導体の性質が電場の定常性を導いているのだと思っています．でも逆に観測的に定常電流が流れていると考えられるからこそ導体の性質がやってくるわけで，卵が先か鶏が先かみたいな話ですね．


閉曲面どこ？


これは前の記事だと不明瞭でした．僕が想定していたのはコンデンサの図における左側の極板です（図の赤点線部分）．
f:id:pandaman64:20151101180715p:plain

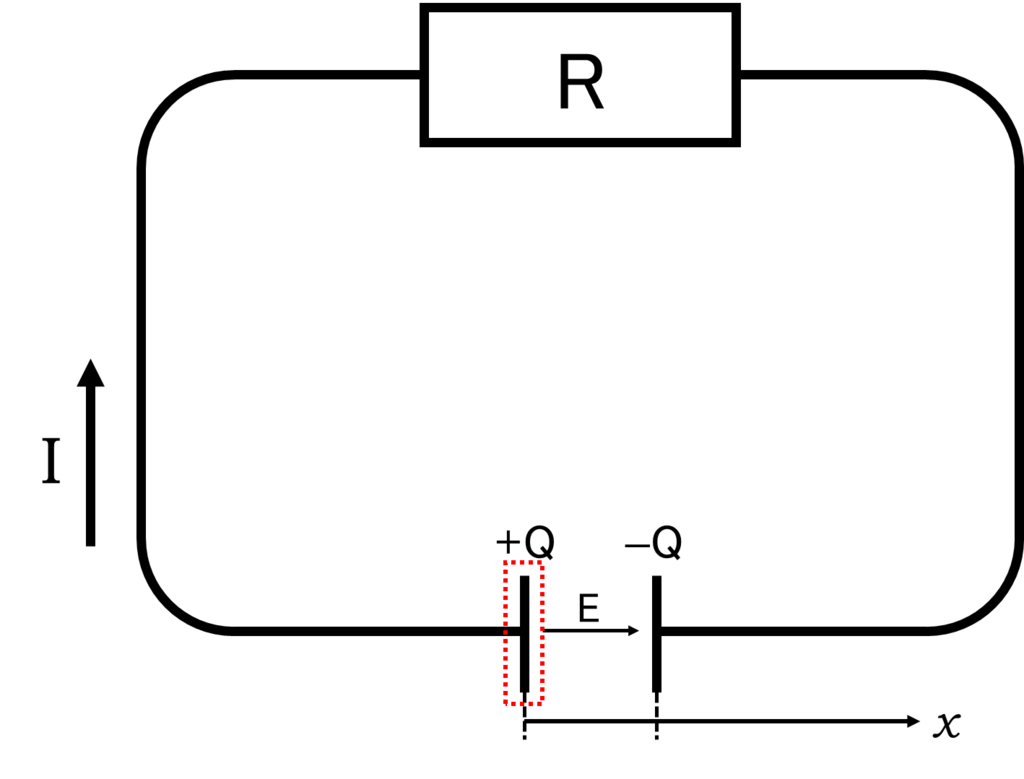
定常状態は電荷密度の定常性も含む


これは定義の仕方の違いですね．僕の立場は定常だと分かっているのは電流だけであるというもので，そこから色々導くために必要な仮定・要請はなんだろうと考えています．

多くの教科書ではこの電荷密度の定常性を仮定に含める立場をとっているみたいです．詳しくは↓pandaman64.hatenablog.jp


外力が系に作用しているから成り立たないのでは


関係ないと思います．定常電流の保存則は局所的に成り立ち（そうでなければキルヒホッフの第一法則は回路の各所で成り立たない），電源の出どころは特に気にしていません．ですから，電池を接続しようがコンデンサをいじろうがピカチュウが10万ボルトを使おうが普遍的に成立するはずです．それに電池といっても化学ポテンシャルを電位に変換する過程は様々であり，それを抽象化して電源と扱うことで理論は成功しているので，ある電位を供給するということ以上の電源の細部は気にする必要がないと思います．

定常電流の保存則の導出

まず，「定常電流の保存則」の保存則には二つの表式があり，それらが表す事象は異なるということに注意する必要がある．

\begin{align} \text{「電荷密度分布は時間について一定」}\quad \frac{\partial \rho}{\partial t} &= 0 \tag{1}\\ \text{「電流の湧き出しは0」}\quad\mathrm{div}\,\boldsymbol{i} &= 0 \tag{2} \end{align}

ここでは，(1)式を電荷についての「定常電流の保存則」，(2)式を電流についての「定常電流の保存則」と呼ぶことにする．

電流についての「定常電流の保存則」の導出

(2)式の方は変位電流を加えれば時間変動によらず成立することがアンペール・マクスウェルの法則から言える．
\begin{align} \text{「アンペール・マクスウェルの法則」}\quad \mathrm{rot}\,\boldsymbol{B} = \mu_0 \boldsymbol{i} + \mu_0 \varepsilon_0 \frac{\partial \boldsymbol{E}}{\partial t} \end{align}
の両辺の\mathrm{div}をとってやれば，\mathrm{div}\,\mathrm{rot}\,\boldsymbol{B}=0なので，
\begin{align} \mathrm{div}\,\boldsymbol{i} + \mathrm{div}\left(\varepsilon_0\frac{\partial \boldsymbol{E}}{\partial t}\right) = 0. \tag{3} \end{align}
変位電流\boldsymbol{i}_dとは，電場の時間変化を仮想的な電流としてみなすもので，これの導入によりアンペールの法則は場が時間変動する場合にも成立するのだった．定義は
\boldsymbol{i}_d = \varepsilon_0 \frac{\partial \boldsymbol{E}}{\partial t}
である．
この表式を導入すれば，(3)式は
\begin{align} \mathrm{div}\,\boldsymbol{i} + \mathrm{div}\,\boldsymbol{i}_d = 0 \tag{3} \end{align}
と書ける．これを「電流の保存則」と呼ぼう．この式は時間変動する場合も成立するので，もちろん定常電流の場合にも成立する．僕が構成した例でも，この法則は成立している（コンデンサの極板における電場の時間変化がちょうど流出する電流と等しくなっているのだ）．

ここで，電場が時間変化しないと仮定すれば，\boldsymbol{i}_d=\boldsymbol{0}となるから
\begin{align} \mathrm{div}\,\boldsymbol{i} = 0 \tag{2} \end{align}
となり，電流についての「定常電流の保存則」が成立する．

この式に「電荷保存則」を適用すれば(1)式（電荷についての「定常電流の保存則」）が導けるのは良いだろう．しかし，電場の定常性を仮定するならば，電荷保存則を仮定しなくとも，電荷についての「定常電流の保存則」は成立するのだ．

電荷についての「定常電流の保存則」の導出

電場の定常性を仮定すれば，ガウスの法則からただちに電荷についての「定常電流の保存則」が導かれる．
\text{「ガウスの法則」}\quad\mathrm{div}\,\boldsymbol{E} = \frac{\rho}{\varepsilon_0}
を時間で微分して，微分の順番を時間と座標で入れ替える．すると，
\mathrm{div}\left(\frac{\partial \boldsymbol{E}}{\partial t}\right) = \frac{1}{\varepsilon_0}\frac{\partial \rho}{\partial t}
であり，電場の定常性を仮定しているのだから\partial \rho/\partial t=0となり，電荷についての「定常電流の保存則」が導かれた．

導出の過程を図に表すと以下の通りになる．
f:id:pandaman64:20151101174047p:plain

結局の所，「定常電流の保存則」は根源的には電場の定常性である．電流の湧き出しと電荷密度の時間変化が0で一致するのはたまたまである（もちろん「電荷保存則」があるからたまたまではないのだが）．

となると気になるのは，どうしてふつうの回路では電場の変動が無いと考えていいのかだ．定常状態の定義に電荷密度分布の定常性が含まれるとする立場では，
\mathrm{div}\left(\frac{\partial \boldsymbol{E}}{\partial t}\right) = \frac{1}{\varepsilon_0}\frac{\partial \rho}{\partial t}
から電場の定常性が導けるかもしれない（本当に言えるか自信がないです）．もしくは，ファインマンがしたように場の定常性も仮定に入れるべきかもしれない．けれども，それはふつうの回路についてもこの議論が適用できることを示さないだろう．そこには，導体の性質などのなんらかの仮定が追加で必要なのではないか．

「定常電流の保存則」とは何なのか

pandaman64.hatenablog.jp の続き．

要約

”定常状態”にはそもそも電荷分布の定常性が含まれるとするのが多数派．

本文

「定常電流の保存則」とは，任意の閉曲面Sに対し，Sを通る電流Iが時間について変化せず一定であるとき，Sが囲む領域内の電荷Qも，時間によらず一定であるという定理である．Sに流れ込む電流をI_{in}，流れ出す電流をI_{out} として図示すると，以下のようになる． f:id:pandaman64:20151031032443p:plain


\begin{align}
\text{「定常電流の保存則」}&\quad
\frac{dI_{in}}{dt} = \frac{dI_{out}}{dt}=0\Rightarrow\frac{dQ}{dt}=0\\
\text{「電荷保存則」}&\quad
\frac{dQ}{dt}=I_{in}-I_{out}
\end{align}

ここで注意しておきたいのは，「定常電流の保存則」は「電荷保存則」とは異なることである．「電荷保存則」は dQ/dt=I_{in}-I_{out} であることを主張しているに過ぎないが，「定常電流の保存則」はこの上でdQ/dt=0，すなわちI_{in}=I_{out} であることを言っているのだ．「電荷保存則」を受け入れたとしても，「定常電流の保存則」は自明ではない．それなのにどうして「定常電流の保存則」を当たり前に受け入れられるだろうか．導体の途中で不良電荷たちがたむろっていてもいいじゃないか（もちろん，キルヒホッフの第一法則がこの保存則を強く示唆していることは分かる）．

図書館で電磁気学と名のつく教科書を片っ端から探し，索引で定常電流の項を引いた．すると，本によってさまざまな流儀で「定常電流の保存則」の成立を説明していた．（ただし，索引に定常電流が載っていない本は見ていないし，一部のテキストでは「電荷の保存則」の項に説明があることもあった．）

説明しないよ派

「定常電流の保存則」の導出や証明を行わない教科書がたくさんあった．以下に例を挙げる．

このようにクーロン力以外に（電池の化学作用のような）非クーロン力をつかうと，時間とともに変わらない電流（これを定常電流という）をつくることができる．定常電流は，電荷自身は移動するがその分布は時間的に変わらないので，その取扱いは静電気の場合とよく似ている． (1)

特に説明はない．個人的には電池だって全部クーロン力だと思うが，他の部分を読んでいないので文脈が分からない．

定常的な磁気減少は，空間内の任意の点で正味の電荷密度の変化が0であるとうい（原文ママ）特徴をもつ．したがって，静磁気学では \begin{equation} \nabla \cdot \boldsymbol{J} = 0 \tag{5.3} \end{equation} が成り立つ． (2)

これも特に説明せず受け入れているが，「定常電流の保存則」についての磁場の関わりを想起させる．

\mathrm{div}\, \boldsymbol{i} + \frac{\partial \rho}{\partial t} = 0 \tag{193} この式は電荷保存則を表しており，電荷に関する連続の式とよばれる．

電流の強さと流れる方向が時間的に変化しない電流を定常電流という．定常電流の場合には \partial \rho/\partial t = 0 であるから \oint_S \boldsymbol{i}\cdot d\boldsymbol{S} = 0 \quad\text{または}\quad \mathrm{div}\, \boldsymbol{i} = 0 \tag{194} である．これを定常電流の保存則という．（引用註：Sは任意の閉曲面） (3)

式で言ってはいるが特に証明があるわけではない．同様なテキストは，たとえば(4)など他の本にもある．

ほかにも，キルヒホッフの第一法則を証明なしに導入する本がいくつかあったが，それもこの態度の表れだろう（キルヒホッフの第一法則は定常電流の保存則によって導かれるため）．

結局，こういったテキストでは「定常電流の保存則」の理解はできないと言わざるを得ないが，誤った説明を載せるよりはなんぼかマシである．

説明になってないよ派

これより，電流保存則 \frac{\partial \rho}{\partial t} + \nabla \cdot \boldsymbol{i} = 0 \tag{4.10.7} が導かれる．

この保存則より定常電流が定義できる．導体線の一部について考えよう．左側からI_1が流れ入り，右端からI_2の電流が出てゆくとする．このとき，電荷の保存則より

\begin{equation} -\frac{dQ}{dt}=I_2-I_1=0 \tag{4.10.8} \end{equation}

である．したがって，I_1=I_2が成り立つ．電流は電場によって引き起こされるから，定常電流では電場も時間的に一定である．（引用註:\rhoは電荷密度で \boldsymbol{i} は電流密度，Qは閉曲面内の電荷） (5)

説明になっていない．「電荷の保存則」は「定常電流の保存則」を導かない（文章内で言うと，I_2-I_1=0が成立するとは限らない．今年出た新しい本なのになあ）．

定常状態は定義に電荷密度の定常性も含むよ派

ここでは明示的に電荷密度の定常性を述べている教科書をとりあげた．説明しないよ派は（暗黙的に）この流儀をとっているのかもしれない．この場合は電荷密度の定常性と電荷保存則から容易に定常電流の保存則が導ける．

電荷密度 \rho(\boldsymbol{r},t) と電流密度 \boldsymbol{J}(\boldsymbol{r},t) は，(5-14)の連続の方程式で関係している： \begin{align} \nabla \cdot \boldsymbol{J} + \frac{\partial \rho}{\partial t} = 0 \tag{5-91} \end{align} 定常電流を考えよう．つまり，\boldsymbol{J} や \rho は空間内いたるところ時間にはよらない．すると，(5-91)により \begin{align} \fbox{定常電流}\quad\nabla \cdot \boldsymbol{J}(\boldsymbol{r}) = 0 \tag{5-92} \end{align} となる．（引用註： \fbox{定常電流} は左寄せ） (6)

定常電流の定義に \rhoの時間について不変である性質が含まれていると読み取れることだろう．この立場をとる他の例にはこのサイトもある．僕の調べた限りでは，僕が通う大学の教科書（後述する）以外のテキストではすべてこの方法を用いて「定常電流の保存則」を導いていた．

これまで挙げたテキストは，定常電流の性質について多くてほんの数行しか言及していないが，『ファインマン物理学』(7)は定常電流について数段落を割いて説明している．

彼の立場でも，電荷密度の定常性を定常状態の定義に含めている．しかし，電荷保存則を用いる方法以外でも「定常電流の保存則」を導いてるのは特徴的だ．どのような方法かというと，電荷密度と電流の定常性を仮定すると，マクスウェル方程式から電場・磁場両方が”静”となることが言えるので，アンペールの法則の両辺の \mathrm{div} をとることで定常電流の保存則を導けるというものだ．この導出は，「電荷保存則」と「定常電流の保存則」が独立であることの一つの証拠となるのではないだろうか．

ほかにも，

\nabla\cdot\boldsymbol{j}=0という要請は電荷はすべて自身閉じている道筋に沿って流れることを意味する．（中略） 回路には電荷を流しつづけるための発電機や電池があってよい．しかし充電や放電をしているコンデンサーがあってはならない．

という記述があり，ファインマン流に言えば僕が構成した例は「定常電流」とは言えないようだ．

この問題とはあまり関係がないが，以下の記述は興味深かった．

”磁場ができるためには本来電流がなくてはならないし，すべての電流は動く電荷からくる．”静磁気”は従って近似である．それは多数の電荷が運動していて，電気の定常な流れで近似されるという特殊な動的状態に関わっている．”

電流の定常性から導けるよ派

大学の教科書(8)では以下のように記述してあって，僕はこれに散々悩まされてこんな長文を書く羽目になったのだった．

電流が時間とともに変化せずに一定の電流が流れる場合，すなわち \frac{dI}{dt} = 0\quad\text{あるいは}\quad\frac{\partial \boldsymbol{i}}{\partial t} = \boldsymbol{0} \tag{4.4} が成り立つとき，これを定常電流(stationary current)という．

導体中を定常電流が流れる場合，電流が時間的に変化しないという条件，すなわち定常電流の条件から，任意の閉曲面内の電荷は変化しない，すなわち \displaystyle{\frac{dQ}{dt}=0} であることがわかる[1]．もしそうでなければ時間とともにその閉曲面内の電荷が変化し，したがって電界も電流も変化するので，定常電流の条件が成り立たなくなるからである．したがって定常電流では，任意の閉曲面Sに対して

\boxed{\iint i_n dS = 0} \tag{4.5} が成り立つ．（引用註： Iは閉曲面Sを流れだす電流， \boldsymbol{i} は電流密度，QはSがなす領域内の電荷，i_nは \boldsymbol{i} の面素dSの法線方向の成分）

とある．電荷の時間変化が電場の時間変化を生むのはガウスの法則からわかるとして，電場の時間変動性はただちに電流の非定常性を導かないよなあとうんうん唸ってたのだ．

それどころか，僕はこの証明が成立しないような反例を構成したわけだが（電場の変化が電流の変化に繋がらないことが僕の例の本質），実はこの文章には以下のような脚注がついていた．

[1][注意]この導体は全体がつながっていることが必要である（強調引用者）．導線の途中でコンデンサーがある場合には導線が途切れているが，この場合には電流が時間的に変化しないとしても，1つの極板を含む閉曲面内ではdQ/dt=\pm I\neq 0となり，以降の議論は適用できない．この場合は8章で考える．（引用註：第8章では変位電流が導入されてマクスウェル方程式が登場する）

というわけで，先生方はすでに問題を分かっていたということだった．ちゃんとテキストは読もう．

しかし，結局のところ定常電流という条件から「定常電流の保存則」が導けるのかは明らかでない．試してみたら，マクスウェル方程式を使えば「定常電流の保存則」の導出できた（と思う…）ので，それはまた別記事に書く．